Startup SaaS : Comment prédire la LTV d’un nouvel utilisateur ?

Lorsque vous travaillez dans une start-up qui détient un produit SaaS, les mêmes problématiques reviennent sans arrêt :

Comment prédire et améliorer la LTV ?

Comment savoir quand un utilisateur va résilier ?

.

Un produit SaaS, pour Service as a Software, c’est une application web pour laquelle on paie (généralement) un abonnement et qui nous rend un service.

Les exemples sont nombreux et c’est un type de business qui explose depuis plusieurs années sur internet :

• Dropbox, ou Google Drive. Vous payez chaque mois pour stocker des données dans le cloud.
• Todoist, Evernote, Trello, Focus@Will, RescueTime, … Ces services qui permettent d’améliorer sa productivité proposent généralement une version gratuite et une version plus évoluée payante.
• Les ESP (Email Service Provider), comme Mailchimp, ConvertKit, Drip, et consorts. Vous payez un abonnement pour avoir une liste d’emails et envoyer facilement des newsletters.
• Les sites de rencontres, où un accès gratuit limité permet de découvrir le produit, puis vous payez chaque mois pour avoir un accès complet.
• Les hébergeurs web
• …

La liste est infinie.

Et les problématiques sont souvent les mêmes.

Par exemple..

Comment savoir combien un nouveau client va nous rapporter ?

C’est ce qu’on appelle la LTV, pour LifeTime Value. On dit aussi CLV : Customer Lifetime Value. C’est la valeur d’un nouveau client.

Selon le produit choisi, les caractéristiques du client, son comportement, on essaie de prédire combien de temps il va utiliser le produit, et combien il va rapporter en moyenne.

Quel est le taux de rétention ?

Le taux de rétention mesure la proportion de clients qui continuent d’utiliser le produit après un certain temps.

Par exemple, un taux de rétention de 50% à 3 mois indique que la moitié des utilisateurs se désengagent au bout de 3 mois.

Il est important de connaître ce taux de rétention, mais aussi de savoir ce qui l’influence afin de pouvoir l’améliorer.

Quels sont les segments de clients les plus profitables ?

Une fois la LTV connue, on s’intéresse à segmenter notre base de clients afin de pouvoir optimiser le produit.

Si on se rend compte qu’une partie de la clientèle rapporte beaucoup moins et tend à se désabonner après 1 mois, on peut faire des économies en arrêtant de les cibler.

Dans cet article, nous allons essayer de répondre à ces questions pour une start-up SaaS qui dispose de 3 années de données sur ses clients.

Présentation de la start-up SaaS

Il s’agit bien entendu d’une start-up virtuelle que nous allons étudier.

Nous disposons de deux jeux de données : customers et subscriptions.

Après nettoyage des données, voici ce dont nous disposons :

Trois ans de données. Entre 2015 et 2017. On imagine qu’on est le 1er janvier 2018 et on veut planifier l’année financière à venir.

100 000 transactions. Plus exactement : 96 528 transactions, parmi 41 971 clients.

Un produit unique. Généralement, on propose plusieurs produits, avec des prix et caractéristiques différents. Là, on va se simplifier la vie et se focaliser sur un produit. Il n’existe pas de version gratuite, donc pas de taux de conversion à prédire.

Trois variables prédictives :

• Le channel d’acquisition, cest-ce que le client est venu de manière organique de Google, ou bien via des publicités payantes ?
• L’appareil utilisé : Le user agent d’un internaute contient généralement pas mal d’informations, notamment si le visiteur utilise un ordinateur ou un mobile.
• Le segment : À l’inscription, l’utilisateur choisit s’il va utiliser le produit en perso ou pour un usage professionnel.

J’ai déjà nettoyé et mergé les données. Voici un aperçu des 5 premières et 5 dernières lignes :

> data
       customer_id first_paid_date channel  device  segment subscription_id
    1:     8010703      2015-01-01    paid unknown    other        15202354
    2:     8010703      2015-01-01    paid unknown    other        17002753
    3:     8010703      2015-01-01    paid unknown    other        18252044
    4:     8010703      2015-01-01    paid unknown    other        19502766
    5:     8010703      2015-01-01    paid unknown    other        23746370
   ---                                                                     
96524:    23450765      2017-12-31    paid  mobile business        28887609
96525:    23451016      2017-12-31 organic  mobile business        28887837
96526:    23451049      2017-12-31    paid  mobile    other        28887884
96527:    23451058      2017-12-31    paid  mobile personal        28887887
96528:    23451104      2017-12-31    paid  mobile business        28887955
       period_start period_end revenue period_length time churn
    1:   2015-01-01 2015-04-01    29.9             3   45 FALSE
    2:   2015-04-01 2015-07-01    29.9             3   45 FALSE
    3:   2015-07-01 2015-10-01    29.9             3   45 FALSE
    4:   2015-10-08 2016-10-08   100.0            12   45 FALSE
    5:   2016-10-08 2018-10-08   120.0            24   45 FALSE
   ---                                                         
96524:   2017-12-31 2018-01-31     1.0             1    1 FALSE
96525:   2017-12-31 2018-01-31     1.0             1    1 FALSE
96526:   2017-12-31 2018-01-31     1.0             1    1 FALSE
96527:   2017-12-31 2018-01-31     1.0             1    1 FALSE
96528:   2017-12-31 2018-01-31     1.0             1    1 FALSE

Explication des variables :

• customer_id : L’identifiant du client
• first_paid_date : La date d’inscription
• channel : Le channel d’acquisition
• device : L’appareil utilisé à l’inscription (mobile/desktop)
• segment : Perso ou business ?
• subscription_id : L’identifiant de la transaction
• period_start : Date de début de la période d’abonnement
• period_end : Date de fin de la période d’abonnement
• revenue : Revenue pour cette période d’abonnement
• period_length : Durée de la période d’abonnement en mois
• time : Temps d’abonnement total
• churn : Le client a-t-il déjà clos son abonnement ?

Notez qu’on est dans un cas très simpliste. On ne dispose ici que de quelques variables prédictives. Dans la vie réelle, on dispose en général de beaucoup plus de données, comme par exemple :

• Davantage de données sur les clients : L’âge, la localisation, la classe sociale, et toutes sortes d’informations qu’il aura rempli lors de son inscription.
• Les interactions entre les clients et le support : On peut potentiellement stocker tous les échanges (écrits ou oraux), leur nombre et fréquence, les classifier pour savoir si les problèmes ont été résolus ou non, si le client râle beaucoup, etc.
• Le comportement du client avec le produit : La fréquence et durée d’utilisation, son évolution dans le temps, etc.

Typiquement, quand on veut prédire le churn, c’est-à-dire quand le client va clôturer son abonnement, on va avoir besoin de ces données supplémentaires pour avoir des prédictions fiables.

Dans le cadre de cet article, on va rester simple et se contenter d’observer le comportement global des clients afin de mieux les comprendre et savoir où concentrer nos ressources. On veut aussi étudier la valeur des clients, et pas seulement prédire le churn.

Étude de la rétention client

Dans un premier temps, concentrons-nous sur ce churn, ou en français, la rétention client.

On va répondre à des questions comme :

• Combien de temps un client reste-t-il en moyenne ?
• Quand un client a-t-il le plus tendance à se désabonner ?
• Quels sont les facteurs influençant le plus la rétention client ?

Pour ça, je vais d’abord agréger le jeu de données pour n’avoir plus qu’une ligne par client :

> data_agg <- unique(data[, .(customer_id, time, churn, channel, device, segment)])
> data_agg
       customer_id time churn channel  device  segment
    1:     8010703   45 FALSE    paid unknown    other
    2:     9173798    3  TRUE organic unknown    other
    3:     9346616   36 FALSE    paid unknown    other
    4:     9650844   27  TRUE    paid unknown    other
    5:     9736636   15  TRUE organic unknown    other
   ---                                                
41967:    23450765    1 FALSE    paid  mobile business
41968:    23451016    1 FALSE organic  mobile business
41969:    23451049    1 FALSE    paid  mobile    other
41970:    23451058    1 FALSE    paid  mobile personal
41971:    23451104    1 FALSE    paid  mobile business

L'approche biaisée

Le problème dans l’étude de la durée moyenne d’abonnement est que l’approche naïve est biaisée.

En effet, ce qu’on aimerait faire, c’est simplement calculer la moyenne de la variable time :

> mean(data_agg$time)
[1] 5.190489

Voire même on pourrait tracer une courbe de la proportion de personnes étant toujours inscrites après 1, 2, 3, … mois :

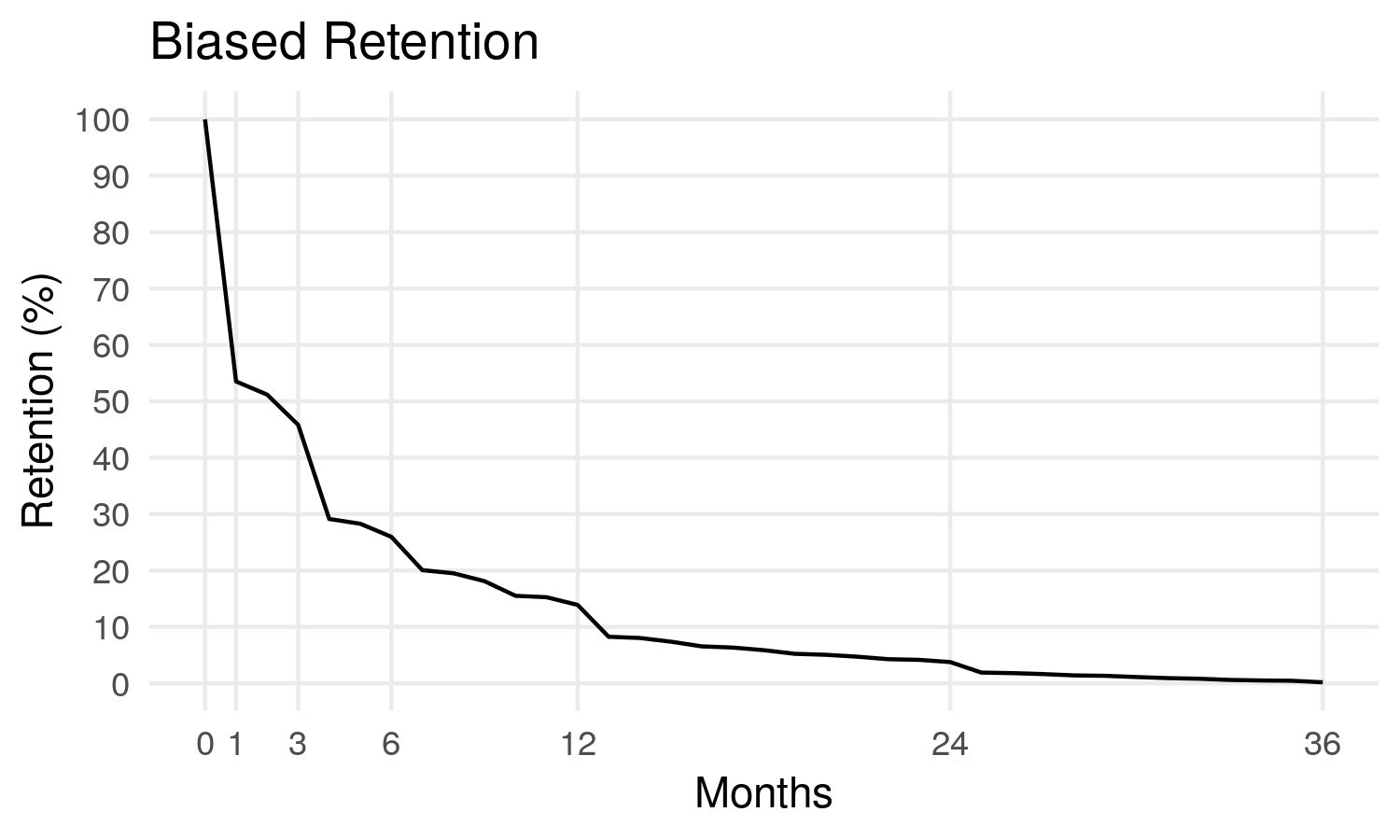
On apprend notamment sur ce graphe que quasiment 50% des abonnés résilient après 1 mois. Et seulement 14% des abonnés restent 12 mois et plus.

Sauf que…

Comme je le mentionnais juste avant, cette approche est biaisée.

En effet, dans notre jeu de données, on a à la fois des clients qui ont déjà résilié, mais aussi d’autres dont l’abonnement est toujours en cours !

Ça veut dire que dans notre estimation, on sous-estime la durée d’abonnement de tous les clients qui n’ont pas encore résilié !

Forcément, on sous-estime donc la moyenne et la rétention…

Alors, que faire ?

L'approche que c'est une mauvaise idée

Une seconde approche pourrait être de ne considérer que les personnes ayant déjà résilié leur abonnement.

Comme ça, plus de sous-estimation !

Sauf que…

> mean(data_agg[churn == TRUE, time])
[1] 3.881243

On obtient une valeur encore plus faible pour la moyenne !

Et puis :

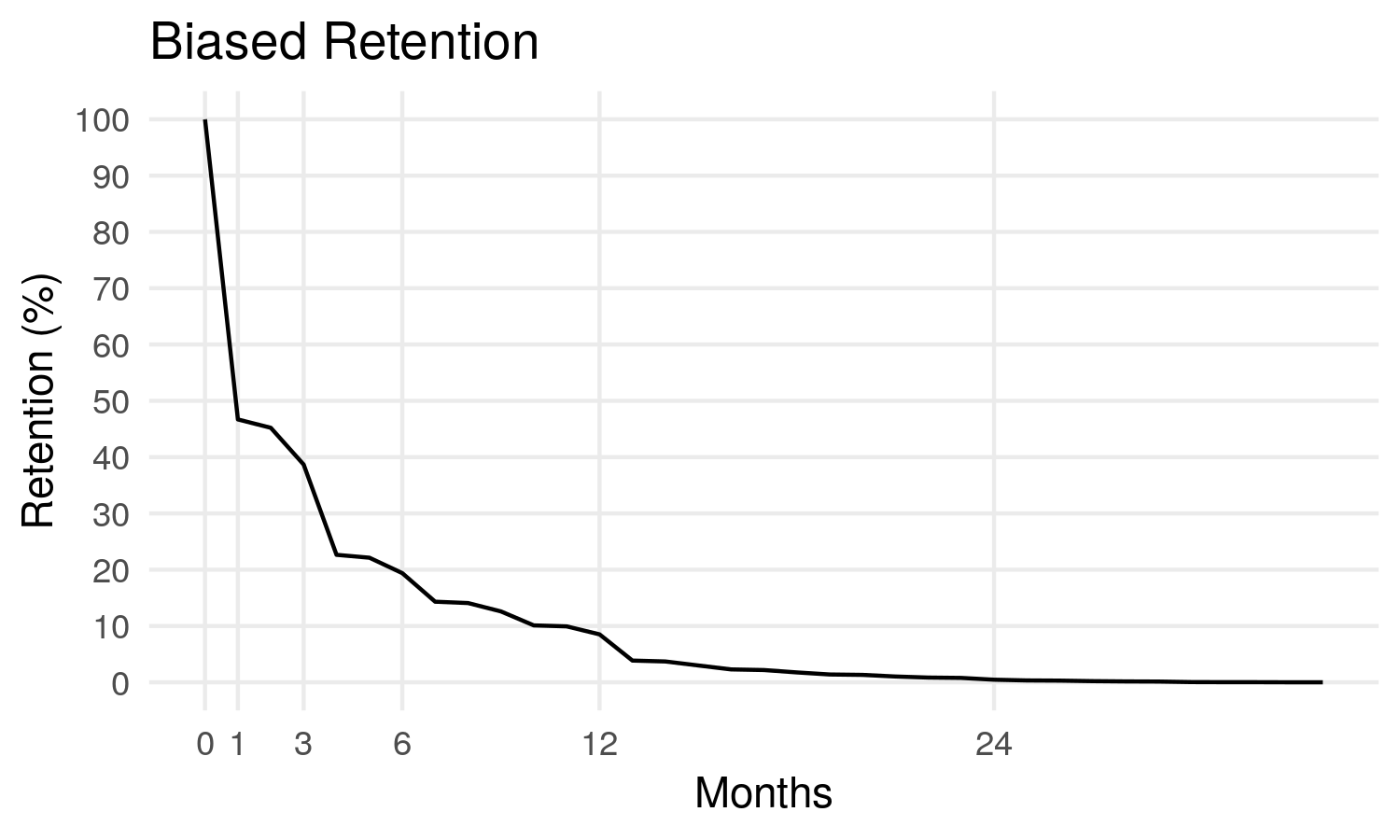
Maintenant, plus de 50% des abonnés résilient après 1 mois, et on arrive à 9% de rétention après 12 mois.

C’est bizarre..

On sous-estime encore plus !

Mais si on y réfléchit..

En fait, en retirant tous les clients ayant déjà résilié, on retire tous ceux qui ont tendance à rester longtemps !

Du coup, on va avoir une sur-représentation des mauvais clients qui partent vite.

Bah oui !

Alors comment faire ?

La bonne approche avec Messieurs Kaplan et Meier

Heureusement, nous ne sommes pas les premiers à faire face à ce problème.

Deux monsieurs y ont déjà réfléchi et ont créé un estimateur qui porte à présent leur nom :

L’estimateur de Kaplan-Meier

Il s’écrit sous la forme suivante :

\[\hat{S}(t) = \prod_{i: t_i \leq t}\left(1 - \frac{d_i}{n_i}\right)\]

avec :

• \(S(t)\) est la fonction de survie. Dans notre contexte, on l’appellerait plutôt la fonction de rétention, c’est exactement ce qu’on essaie d’estimer depuis tout à l’heure et qu’on a tracé à deux reprises plus haut.
• \(\prod\) est le symbole du produit (la multiplication). Pour une valeur de temps \(t\), on multiplie l’expression entre parenthèses pour chaque donnée \(i\) où \(t_i\) est inférieur à \(t\).
• \(d_i\) est le nombre de résiliations au temps \(t_i\).
• \(n_i\) est le nombre d’abonnés restants au temps \(t_i\).

Si les mathématiques vous dépassent, rassurez-vous, on va vite revenir à des explications plus concrètes avec des dessins ! Le but n’est pas de rentrer trop en avant dans les maths.

Le GROS avantage de cet estimateur est qu’il prend en compte le fait que les abonnés qui n’ont pas encore résilié vont potentiellement rester plus longtemps.

Il s’agit en fait de l’estimateur du max de vraisemblance, ce qui garantit qu’il a de bonnes propriétés, et notamment qu’il est asymptotiquement sans biais.

Comparons à présent nos 3 estimateurs :

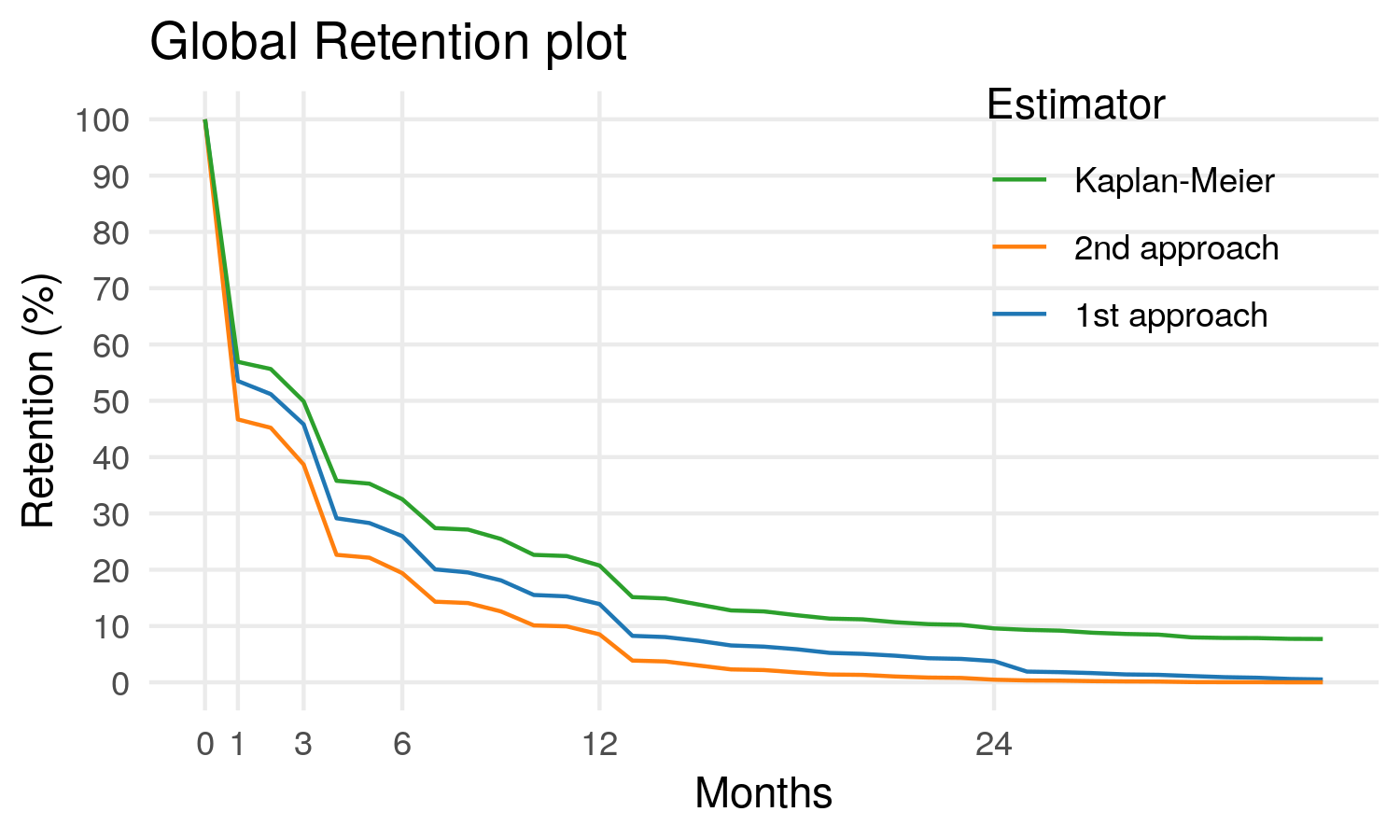
On observe à présent qu’effectivement, les deux estimateurs précédemment étudiés sous-estiment largement la rétention !

On peut recalculer la moyenne grâce à la formule utilisant la fonction de répartition :

> sum(data_surv$surv) / 100
[1] 8.243749

Et pour comparer avec les valeurs utilisés précédemment, on a à présent seulement 43% des abonnés résiliant après 1 mois, et une rétention à 12 mois de 21%.

Des chiffres complètement différents !

Mais qui cette fois-ci prennent bien tout l’échantillon en compte, ainsi que le fait que les utilisateurs n’ayant pas résilié vont potentiellement rester plus longtemps.

D'autres résultats intéressants :

On remarque aussi que :

La médiane se situe à 3 mois

Ce qui signifie que 50 % des clients vont résilier dans les 3 premiers mois.

Qu’est-ce qui explique ce désengagement si rapide ?

Est-ce que le produit est trop difficile à utiliser pour certains types de clients ?

Est-ce qu’on peut identifier un segment particulier représentant ces early leavers ?

À creuser.

Les périodes de désengagement les plus importantes…

sont après 1 mois (43%), 4 mois (14%), 7 mois (5%) et 13 mois (6%).

Si on jette un rapide coup d’œil, on s’aperçoit d’un comportement récurrent :

L’utilisateur s’inscrit d’abord pour 1 mois, il est satisfait et prolonge son abonnement avec une ou plusieurs périodes de 3, 6 ou 12 mois (puisque ça lui revient moins cher que de payer mois par mois).

Donc nécessairement, le moment où il se désinscrit tombe sur 1, 4, 7, 13, etc.

Il convient donc de particulièrement accompagner le client lorsque ces périodes fatidiques approchent.

Suite ?

Dans cet article, on a commencé à étudier la rétention, mais on n’a pas répondu à toutes les questions !

Il nous reste encore à expliquer :

• Quels sont les facteurs influençant le plus la rétention client ?
• Quels sont les segments les plus profitables ?
• Comment estimer la valeur d’un nouveau client ?
• Comment estimer la valeur du pool total de clients existants ?
• …

Nous répondrons à ces questions dans de futurs articles !