L’Algèbre Linéaire pour la Data Science : Pourquoi ?

Cet article fait partie de la série L’algèbre linéaire pour la Data Science, divisée en 18 parties. Pour accéder aux autres parties, utilisez le sommaire ci-dessous :

• Partie 0 : Pourquoi l’algèbre linéaire pour la Data Science ?
• Partie 1 : Les trois définitions d’un vecteur
• Partie 2 : Combinaisons linéaires, espaces engendrés, et bases
• Partie 3 : Transformations linéaires et matrices
• Partie 4 : Multiplication matricielle
• Partie 5 : Le déterminant
• Partie 6 : Images, noyaux, inverses
• Partie 7 : Matrices rectangulaires
• Partie 8 : Matrices spéciales
• Partie 9 : Produit scalaire et dualité
• Partie 10 : Produit vectoriel
• Partie 11 : Changement de base
• Partie 12 : Vecteurs propres et valeurs propres
• Partie 13 : Décomposition en valeurs singulières (SVD)
• Partie 14 : Les normes
• Partie 15 : Pseudo-inverse de Moore-Penrose
• Partie 16 : La trace
• Partie 17 : Analyse en Composante Principale (PCA)

---

Lorsque je crée des cours autour de la data science, on me demande souvent :

Quels sont les pré-requis à connaître en mathématiques ?

Et ma réponse est souvent un peu vague : Ça dépend.

C’est vrai, ça dépend !

La réalité, c’est qu’on peut très bien faire de la data science avec seulement des connaissances de mathématiques de niveau lycée.

D’ailleurs, j’ai même créé un cours de Deep Learning où quasi aucune connaissance de maths n’est requise.

L’idée c’est justement de se focaliser sur le côté intuitif de la théorie, et surtout de faire beaucoup de pratique.

Du coup, pas de maths.

Mais si vous souhaitez aller au-delà du simple fait d’appliquer des algorithmes au hasard et si vous prenez votre carrière de data scientist au sérieux… il va falloir s’y coller.

Note : Cet article introductif parle de plusieurs concepts d’algèbre linéaire. Si vous n’en avez jamais fait, soyez rassuré, nous reverrons tout de la base à partir du prochain chapitre. Les seules connaissances mathématiques requises pour suivre cette série sont de niveau lycée.

À quoi ça sert l'Algèbre Linéaire ?

Donc.. pourquoi ?

Quand j’étais petit, à l’école, j’aimais pas trop ça l’algèbre linéaire.

C’était beaucoup de théorèmes beaucoup trop abstraits pour moi (“théorème spectral”.. vraiment ?!), je ne comprenais pas pourquoi on faisait ça, ni à quoi ça pouvait bien servir, et surtout, je n’avais aucune intuition autour de ce que j’apprenais.

En gros.. j’étais largué.

Mais récemment.. je m’y suis remis.

J’ai décidé que quand même ce serait cool si j’arrivais à comprendre ce que je faisais.

Alors pourquoi ?

Tous les algorithmes utilisés en machine learning s’appuient sur l’algèbre linéaire

Tous.

Et c’est aussi valable pour tous les modèles statistiques.

Prenez par exemple la régression.

Le modèle le plus simple du modèle.

On trace une droite au milieu d’un nuage de points.

Croyez-moi, on n’a pas attendu l’arrivée des stats et Legendre pour tracer une droite au milieu d’un nuage de points !

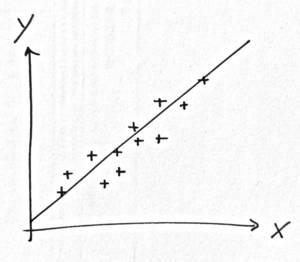
Comment on la trace cette droite ?

Intuitivement, c’est facile. On voit bien où devrait passer la droite.

Mais.. mathématiquement ?

L’idée, c’est de minimiser les distances verticales entre les points et la droite.

Donc, si on a une droite \(y = \beta_0 x + \beta_1\), on cherche à connaître \(\beta_0\) et \(\beta_1\).

Pour y arriver, on va minimiser l’expression suivante :

\[\sum_{i=1}^n (y_i - \beta_0 - \beta_1 x_i)^2\]

Ensuite, on calcule les dérivées partielles en \(\beta_0\) et en \(\beta_1\), on résout les équations de ces dérivées égales à 0, et c’est tout !

Alors..

..où sont les stats ?

.

Nulle part.

Pas de calcul de moyenne, pas d’écart-type, pas de loi statistique, pas d’intervalle de confiance, rien de tout ça.

Juste une simple résolution d’équation.

Je peux même faire des prédictions grâce à cette droite !

Mais alors.. pourquoi on dit que faire une régression c’est des statistiques ?

Pourquoi on nous embête avec des trucs compliqués comme des variables aléatoires et des lois normales ?

En fait, on aura besoin des statistiques seulement si on veut aller plus loin.

Si on veut faire un intervalle de confiance par exemple.

Ou si on veut connaître les propriétés de notre estimateur. Son biais, sa convergence, sa variance. Ce genre de choses.

Et ça c’est important aussi !

Mais..

Pour minimiser la somme plus haut ?

Pas besoin.

En fait, tout ce dont j’ai besoin…

.

.

C’est de l’algèbre linéaire !

En effet, la résolution d’équation qu’on a faite, c’est de l’algèbre linéaire.

Ça n’a pas l’air comme ça, mais on a d’abord projeter un espace à 2 dimensions sur un espace à 1 dimension et ensuite on a calculé un Jacobien.

Ça se voit pas parce que c’est un exemple simple, mais si on avait une régression multiple à \(p\) variables, ce serait plus évident.

Donc retenez bien :

Tous les algorithmes de machine learning et tous les modèles de statistique utilisent l’algèbre linéaire.

Et tous, c’est tous. Sans exception.

Pourquoi s'y intéresser ?

Qui ici sait faire une ACP ?

Qui ici comprend la théorie derrière l’ACP et est capable de l’expliquer ?

Ok. (On se calme dans le fond !)

Maintenant, on se comprend.

Si vous vous trouvez dans la première catégorie et pas dans la deuxième, il n’y a vraiment aucune honte à avoir.

J’étais dans cette situation jusqu’à récemment.

(Et si vous n’avez pas levé votre main du tout, c’est pas grave, on est là pour apprendre !)

Et c’est toujours le cas pour plein d’autres sujets que l’ACP.

La raison est simple.

Comment faire une ACP ?

pca <- prcomp(data, scale = TRUE)

Une ligne de code.

Comment expliquer l’ACP ?

Cette prise d’écran est extraite du livre Deep Learning de I. Goodfellow, Y. Bengio, et A. Courville, chapitre 2 Linear Algebra sur l’ACP.

Trois pages de charabia.

Forcément, ça paraît moins cool.

Et quand le client demande de faire une ACP, est-ce que vraiment on va s’amuser à se taper toute la théorie quand il existe des fonctions toutes préparées qui le font pour nous ?

Eh bien oui. Et la raison est double.

D’abord, je ne sais pas pour vous, mais perso ça me gène pas mal de dire que je suis data scientist, d’appliquer tous les jours des techniques d’exploration ou de prédiction de données… et de ne rien comprendre à ce que je fais.

Ou en tout cas d’être incapable de l’expliquer.

Ça me rappelle cette image qu’on voyait partout pendant un moment :

Image trouvée sur les internets

Ben non.

C’est un peu nul de passer pour un type qui ne fait qu’appliquer des algos déjà codés.

Ça me donne juste l’impression d’être une fraude.

Et en plus en vrai ma job est un peu plus compliqué que ça, si je la fais bien !

Pas fun.

La deuxième raison, c’est que justement quand on nous embauche pour faire de la data science, on attend de nous davantage que juste aligner du code.

Récemment, un client m’a demandé d’aller au-delà de simplement appliquer une ACP.

J’ai dû sortir des résultats que les librairies de R ne me donnaient pas automatiquement !

Et là je me suis senti con parce que j’ai dû faire autre chose que juste appuyer sur un bouton.

Du coup, j’ai pris ça comme une opportunité.

Je me suis replongé dans l’ACP, comment ça marche, pourquoi, qu’est-ce qu’on peut faire avec, etc.

Et c’était super cool !

J’avais déjà appris ça à l’école, sauf que j’avais vite tout oublié.

C’était non seulement chouette de revoir ces bases, mais en plus j’ai pu répondre à la demande de mon client.

Et l’ACP, c’est purement de l’algèbre linéaire !

On s’en reparlera dans quelques épisodes puisque j’ai prévu de faire un article entier dessus !

C'est quoi l'algèbre linéaire en fait ?

C’est marrant, parce que quand j’étais petit, à l’école, j’ai jamais compris ce que voulait dire ce terme.

En première année de prépa, on nous a sorti ce nouveau terme… linéaire.

C’est quoi linéaire ?

J’ai rapidement compris que certaines fonctions n’étaient pas linéaires.

Sinus, cosinus, la racine carrée, l’exponentielle, le logarithme… Pas linéaire.

J’ai aussi rapidement compris que quand on faisait que des additions, c’était linéaire.

Mais une vraie définition claire et précise ?

On a vu une définition exacte un peu plus tard dans l’année.

Je vous la donne juste pour illustrer, d’après Wikipédia :

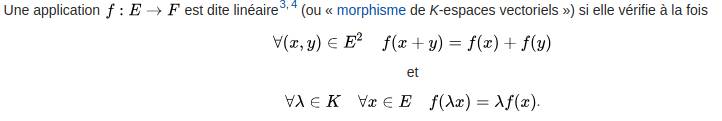
Cool, non ?

Non.

:(

Pas vraiment immédiat.

Mon objectif, dans cette série d’articles, c’est d’aller au-delà de ce genre de définitions.

Je préfère les définitions plus intuitives, certes moins rigoureuses, mais compréhensibles.

.

Une fonction est linéaire si elle est sous la forme \(f(x) = ax\).

Et le terme linéaire vient de ligne.

Vous aurez remarqué que l’équation qu’on vient juste d’écrire est celle d’une droite qui passe par l’origine.

Ça marche aussi avec plusieurs variables : \(f(x, y) = ax + by\).

Ça c’est l’équation d’un plan (qui passe par l’origine).

L’algèbre linéaire, c’est l’étude de ces fonctions.

Tout simplement.

Après, en pratique, ces fonctions sont dans des espaces à \(m\) et \(n\) dimensions.

D’ailleurs, on peut voir cette définition géométriquement. Et là ça devient vraiment fun !

Si si ! Pour de vrai !

Une fonction (ou transformation) dans le plan, elle va transformer le plan en quelque chose de différent.

On peut dire qu’une transformation est linéaire si elle vérifie deux propriétés :

1. Toutes les lignes restent des lignes
2. L’origine reste à l’origine.

Voyez par vous-même un exemple la transformation suivante :

\[f(x, y) = \left\{ \begin{array}{rcl} 2x & + & y \\ x & + & y \end{array} \right.\]

Par exemple, cette transformation va emmener le point \((1, 1)\) vers les coordonnées \((3, 2)\).

Si on prend tous les points d’une ligne, alors ces points une fois transformés forment toujours une ligne.

Et comme elle garde l’origine \((0, 0)\) au même point \((0, 0)\), on en conclut que c’est une transformation linéaire.

Voici à quoi elle ressemble :

Regardons un exemple qui cette fois-ci n’est PAS linéaire :

\[f(x, y) = \left\{ \begin{array}{l} cos(x) \\ sin(x) \end{array} \right.\]

D’abord l’origine bouge, cette fois-ci, elle se retrouve aux coordonnées \((1, 0)\).

Et puis clairement, les lignes ne sont plus des lignes !

Pas linéaire.

.

On reverra tous ces concepts dans de futurs chapitres.

Pour l’instant, tout ce qu’il faut retenir, c’est que l’algèbre linéaire, c’est l’étude des transformations où les lignes restent des lignes.

Et rien qu’avec ça…

On peut déjà faire pas mal de choses !

Si vous avez l’eau à la bouche et êtes assoiffé d’en savoir plus.. alors n’hésitez plus et jetez-vous sur le premier chapitre :

Partie 1 : Les trois définitions d’un vecteur (à venir)